Zone Axis on:
[Wikipedia]
[Google]
[Amazon]
 Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
pdf
/ref> Direct lattice vectors have components measured in distance units, like
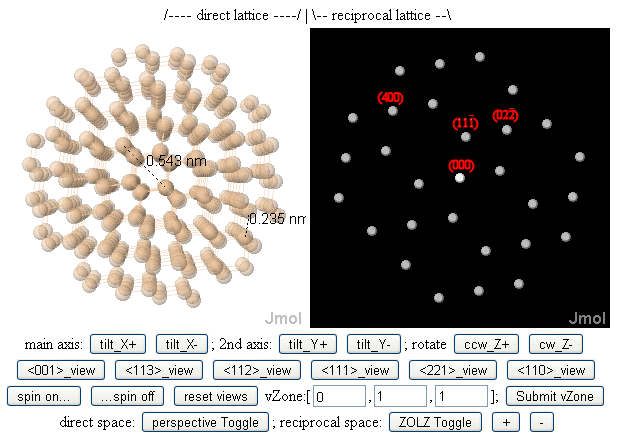 One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low-
One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low-
preview
David B. Williams and C. Barry Carter (1996) ''Transmission electron microscopy: A textbook for materials science'' (Plenum Press, NY) P. Hirsch, A. Howie, R. Nicholson, D. W. Pashley and M. J. Whelan (1965/1977) ''Electron microscopy of thin crystals'' (Butterworths/Krieger, London/Malabar FL)
International Tables for Crystallography
Materials science Crystals Electron microscopy Crystallography Diffraction
 Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the reciprocal lattice
In physics, the reciprocal lattice represents the Fourier transform of another lattice (group) (usually a Bravais lattice). In normal usage, the initial lattice (whose transform is represented by the reciprocal lattice) is a periodic spatial fu ...
) of a crystal in three dimensions. It is therefore indexed with direct lattice indices, instead of with Miller indices
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.
In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers ''h'', ''k'', and ''â ...
.
High-symmetry zone axes through a crystal lattice, in particular, often lie in the direction of tunnels through the crystal between planes of atoms. This is because, as we see below, such zone axis directions generally lie within more than one plane of atoms in the crystal.
Zone-axis indexing
Thetranslational invariance
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equatio ...
of a crystal lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n ...
is described by a set of unit cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessaril ...
, direct lattice basis vectors
In mathematics, a set of vectors in a vector space is called a basis if every element of may be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as componen ...
( contravariantGeorge Arfken (1970) ''Mathematical methods for physicists'' (Academic Press, New York). or polar
Polar may refer to:
Geography
Polar may refer to:
* Geographical pole, either of two fixed points on the surface of a rotating body or planet, at 90 degrees from the equator, based on the axis around which a body rotates
* Polar climate, the c ...
) called a, b, and c, or equivalently by the lattice parameters, i.e. the magnitudes of the vectors, called ''a'', ''b'' and ''c'', and the angles between them, called ''α'' (between b and c), ''β'' (between c and a), and ''γ'' (between a and b).J. M. Ziman (1972 2nd ed) ''Principles of the theory of solids'' (Cambridge U. Press, Cambridge UK).Zbigniew Dauter and Mariusz Jaskolski (2010) "How to read (and understand) Volume A of International Tables for Crystallography: an introduction for nonspecialists", ''J. Appl. Crystallogr.'' 43, 1150–117/ref> Direct lattice vectors have components measured in distance units, like
meters
The metre (British spelling) or meter (American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its prefi ...
(m) or angstrom
The angstromEntry "angstrom" in the Oxford online dictionary. Retrieved on 2019-03-02 from https://en.oxforddictionaries.com/definition/angstrom.Entry "angstrom" in the Merriam-Webster online dictionary. Retrieved on 2019-03-02 from https://www.m ...
s (Ã…).
A lattice vector is indexed by its coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
in the direct lattice basis system and is generally placed between square brackets []. Thus a direct lattice vector , or , is defined as . Angle brackets ⟨⟩ are used to refer to a symmetrically equivalent class of lattice vectors (i.e. the set of vectors generated by an action
Action may refer to:
* Action (narrative), a literary mode
* Action fiction, a type of genre fiction
* Action game, a genre of video game
Film
* Action film, a genre of film
* ''Action'' (1921 film), a film by John Ford
* ''Action'' (1980 fil ...
of the lattice's symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient ...
). In the case of a cubic lattice, for instance, ⟨100⟩ represents 00 10 01 0 0and 0because each of these vectors is symmetrically equivalent under a 90 degree rotation along an axis. A bar over a coordinate is equivalent to a negative sign (e.g., ).
The term "zone axis" more specifically refers to the direction of a direct-space lattice vector. For example, since the 20and 40lattice vectors are parallel, their orientations both correspond the ⟨120⟩ zone of the crystal. Just as a set of lattice plane In crystallography, a lattice plane of a given Bravais lattice is any plane containing at least three noncollinear Bravais lattice points. Equivalently, a lattice plane is a plane whose intersections with the lattice (or any crystalline structure of ...
s in direct space corresponds to a reciprocal lattice
In physics, the reciprocal lattice represents the Fourier transform of another lattice (group) (usually a Bravais lattice). In normal usage, the initial lattice (whose transform is represented by the reciprocal lattice) is a periodic spatial fu ...
vector in the complementary space of spatial frequencies
In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier tra ...
and momenta, a "zone" is definedE. W. Nuffield (1966) ''X-ray diffraction methods'' (John Wiley, NY).B. E. Warren (1969) ''X-ray diffraction'' (Addison-Wesley, paperback edition by Dover Books 1990) . as a set of reciprocal lattice planes in frequency space
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a sig ...
that corresponds to a lattice vector in direct space.
The reciprocal space analog to a zone axis is a "lattice plane normal Normal(s) or The Normal(s) may refer to:
Film and television
* ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson
* ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum Keith Rennie, and Andrew Airlie
* ''Norma ...
" or "g-vector direction". Reciprocal lattice vectors (one-form
In differential geometry, a one-form on a differentiable manifold is a smooth section of the cotangent bundle. Equivalently, a one-form on a manifold M is a smooth mapping of the total space of the tangent bundle of M to \R whose restriction to ea ...
cf. Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973) ''Gravitation'' (W. H. Freeman, San Francisco CA). or axial) are Miller-indexed using coordinates in the reciprocal lattice basis instead, generally between round brackets () (similar to square brackets [] for direct lattice vectors). Curly brackets (not to be confused with a mathematical Set (mathematics)#How sets are defined and set notation, set) are used to refer to a symmetrically equivalent class of reciprocal lattice vectors, similar to angle brackets ⟨⟩ for classes of direct lattice vectors.
Here, , , and , where the unit cell volume is ( denotes a dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
and a cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
). Thus a reciprocal lattice vector or has a direction perpendicular to a crystallographic plane and a magnitude equal to the reciprocal of the spacing between those planes, measured in spatial frequency units, e.g. of cycles per angstrom (cycles/Ã…).
A useful and quite general rule of crystallographic " dual vector spaces in 3D", e.g. reciprocal lattices, is that the condition for a direct lattice vector 'uvw''(or zone axis) to be perpendicular to a reciprocal lattice vector (''hkl'') can be written with a dot product as . This is true even if, as is often the case, the basis vector set used to describe the lattice is not Cartesian Cartesian means of or relating to the French philosopher René Descartes—from his Latinized name ''Cartesius''. It may refer to:
Mathematics
*Cartesian closed category, a closed category in category theory
*Cartesian coordinate system, modern ...
.
Zone-axis patterns
By extension, a 'uvw''zone-axis pattern (ZAP) is adiffraction
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
pattern taken with an incident
Incident may refer to:
* A property of a graph in graph theory
* ''Incident'' (film), a 1948 film noir
* Incident (festival), a cultural festival of The National Institute of Technology in Surathkal, Karnataka, India
* Incident (Scientology), a ...
beam, e.g. of electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no kn ...
s, X-ray
An X-ray, or, much less commonly, X-radiation, is a penetrating form of high-energy electromagnetic radiation. Most X-rays have a wavelength ranging from 10 picometers to 10 nanometers, corresponding to frequencies in the range 30&nb ...
s or neutron
The neutron is a subatomic particle, symbol or , which has a neutral (not positive or negative) charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons beh ...
s traveling along a lattice direction specified by the zone-axis indices 'uvw'' Because of their small wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, tro ...
''λ'', high energy electrons used in electron microscope
An electron microscope is a microscope that uses a beam of accelerated electrons as a source of illumination. As the wavelength of an electron can be up to 100,000 times shorter than that of visible light photons, electron microscopes have a hi ...
s have a very large Ewald sphere The Ewald sphere is a geometric construction used in electron, neutron, and X-ray crystallography which demonstrates the relationship between:
:* the wavevector of the incident and diffracted x-ray beams,
:* the diffraction angle for a given ref ...
radius (1/λ), so that electron diffraction generally "lights up" diffraction spots with g-vectors (''hkl'') that are perpendicular to 'uvw''John M. Cowley (1975) ''Diffraction Physics'' (North-Holland, Amsterdam).
 One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low-
One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low-Miller index
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.
In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers ''h'', ''k'', and ''â„ ...
" lattice planes, which in turn have small spatial frequencies (g-values) and hence large lattice periodicities (d-spacings). A possible intuition behind this is that in electron microscopy, for electron beams to be directed down wide (i.e. easily visible) tunnels between columns of atoms in a crystal, directing the beam down a low-index (and by association high-symmetry) zone axis may help.J. W. Edington (1976) ''Practical electron microscopy in materials science'' (N. V. Philips' Gloeilampenfabrieken, Eindhoven) Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, Berlinpreview
David B. Williams and C. Barry Carter (1996) ''Transmission electron microscopy: A textbook for materials science'' (Plenum Press, NY) P. Hirsch, A. Howie, R. Nicholson, D. W. Pashley and M. J. Whelan (1965/1977) ''Electron microscopy of thin crystals'' (Butterworths/Krieger, London/Malabar FL)
See also
*Crystallography
Crystallography is the experimental science of determining the arrangement of atoms in crystalline solids. Crystallography is a fundamental subject in the fields of materials science and solid-state physics (condensed matter physics). The wor ...
* Dual basis
In linear algebra, given a vector space ''V'' with a basis ''B'' of vectors indexed by an index set ''I'' (the cardinality of ''I'' is the dimension of ''V''), the dual set of ''B'' is a set ''B''∗ of vectors in the dual space ''V''∗ with th ...
* Reciprocal lattice
In physics, the reciprocal lattice represents the Fourier transform of another lattice (group) (usually a Bravais lattice). In normal usage, the initial lattice (whose transform is represented by the reciprocal lattice) is a periodic spatial fu ...
* Miller index
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.
In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers ''h'', ''k'', and ''â„ ...
* Diffraction
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
* Electron diffraction
Electron diffraction refers to the bending of electron beams around atomic structures. This behaviour, typical for waves, is applicable to electrons due to the wave–particle duality stating that electrons behave as both particles and waves. Si ...
* Transmission electron microscopy
Transmission electron microscopy (TEM) is a microscopy technique in which a beam of electrons is transmitted through a specimen to form an image. The specimen is most often an ultrathin section less than 100 nm thick or a suspension on a g ...
Footnotes
{{ReflistExternal links
International Tables for Crystallography
Materials science Crystals Electron microscopy Crystallography Diffraction